Coriolis effect and drains
on Friday, October 11, 2013It's a widely held belief that water from a drain turns in one direction in the northern hemisphere and counterclockwise in the southern hemisphere. And in the equator... I don't know, It doesn't turn in the equator, it just falls straight down I guess. Those who want to go a little further and are able to remember the name, normally attribute this effect to a mysterious Coriolis effect. Although probably they are not able to explain what it is, the fact that it relates to a scientific theory seems enough to give credibility without actually checking if this relationship is real, although anyone can try it at home: just pull the plug and look how the water falls.
The proof... or not
You can actually see exhibits on the line of the equator that try to prove so: they empty a sink above the line of equator and the water falls straight down the drain. After moving a few meters to one hemisphere, the water falls turning around the drain. Finally, they move a few meters across the equator to the other hemisphere, and water falls spinning in the other direction.
The first problem I encounter to believe this experiment is that I have to accept that the line painted on the floor marks the separation between the north and south hemispheres with an accuracy of about one meter, since this alleged difference between north and south hemispheres is observed by only moving a couple of meters across this line. The other problem I find is that this radical change about water always turning in one direction and just crossing the equator behaving totally different and turning in the other direction sounds almost like magic, doesn't it?
But hey, let's be complacent and forget these points. There is a more serious problem: the three tests are not performed with the same conditions. To verify that a given variable is the cause that produces an effect you have to keep constant the other factors that can also alter the result, and that is not being done in this experiment. Apart from the location of the sink, there is another important factor that is being changed: the state of repose or initial movement of the water. We see that in the first test, performed "above" of the equator, the water is at rest (more or less). In the second, as the water is poured, the bucket is moved to the left (clockwise) and in the third, they throw the water moving the bucket to the right (counterclockwise).
Also note that they throw some leaves to the water so you can see how the water falls down the drain in the predicted direction. But they throw them after opening the drain so you can't see that the water was already in motion before opening the drain. For the same reason, they remove all the leaves before making the next test, so you can't note they are cheating when they throw the water.
And that initial movement they apply is just the same the water haves as it falls down the drain. The water is just keeping the same movement initially applied to it, and as the circumference of the rotation gets smaller as it approaches the drain, it will increase its speed (conservation of angular momentum).
Well, you see that in this typical demonstration they are cheating, but that doesn't mean that without that initial movement we won't get the same result. Have you tested it? Have you asked to prove it to the person that told you? Does water always fall in the direction predicted by the hypothesis in all the drains at your home? Notice that I emphasized "all" and "always" as the urban legend says that the water drains in the northern hemisphere turn in one direction and in the south always in the opposite direction, as a kind of physical law "explained" by the unexplained Coriolis effect. So, by finding a single case which doesn't fulfill, we will void the hypothesis.
I have myself done the same test and, oh, surprise, without moving from my home in the Spanish northwest I made the water turn clockwise when it is assumed that in the northern hemisphere should always turn counterclockwise:
In case you still have doubts, I also managed to turn it counterclockwise:
That is, without changing hemisphere, I managed to turn it in both directions. Is not supposed that water should always rotate in the same direction unless we change hemisphere? How did I do it? Well as you can see in the video, using the same cheat as in the initial video: by applying an initial movement in the direction that I am interested in.
If we do not apply enough initial movement (in a "homespun" experiment like this one is inevitable to apply disturbances when you pull the plug), I see no movement in the drain, which supposedly only happens in the equator:
So, does water turn always in the same direction in each of the hemispheres when going down the drain? Not really. Sometimes it turns in one direction and sometimes in the other one, it depends on various factors such as the shape and position of the basin, the plug position, the initial state of the water, ... Well, what then? Is the Coriolis effect fake? No, Coriolis effect exists and is very important for example in air travel, storms and tides. To a lesser extent, it theoretically influences the water drain, but its influence is so weak that it is nullified by other factors and even if we cancel these other factors, the influence of the Coriolis effect is too weak to be perceptible:
The question, then, is whether the Coriolis effect could be detected in the water of my basin. The answer is yes, and in fact, it has been achieved. If you have a circular sink over a meter in diameter filled with water completely still (except, of course, by the rotation of the Earth) with a tiny hole in its precise geometric center obstructed by a plug reachable from the bottom so as not to introduce spurious movements in the liquid, and had the entire system in a non-seismic and totally free of vibration area, it could be tested. You have to let the water settle for at least a week (or, better, for one month) for the molecules to lose all motion and then gently remove the bottom plug. Water will begin to flow through the small hole, emptying the tank, and if the process continues for 14 or 20 hours, we will see that gradually the Earth's rotation begins to introduce small deviations in the flow of fluid to achieve a circular motion. The motion is clearly cyclonic type, and rotates clockwise in our southern hemisphere and counterclockwise in the northern hemisphere. — Dos Santos, Marcelo. "La "verdad" mentirosa" [translated by me]. Axxón. Num. 139 (june 2004)
The Coriolis effect
It is not my intention to give a very precise and deep explanation of the topic. First of all, because then another one will have to do it, and secondly because this article is not written for graduates in physics but for the general public who has the widespread belief that water swirls in different directions in each hemisphere. For this reason, I will use some terms that can squeak the most orthodox people but that will make easier their understanding, such as the Earth "escaping" of the airplanes after "pushing them" or that the Earth rotates at different speeds depending on the latitude. In the latter, I obviously mean linear speed, but will omit this clarification from now on.
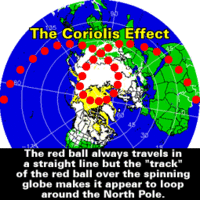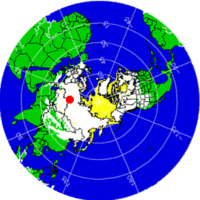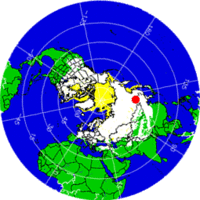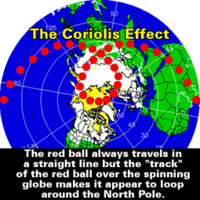
We could describe the Coriolis effect as the apparent deviation of a straight path that an observer perceives from a system in rotation whose axis of rotation is perpendicular to that said straight path.
As usual, everything is best understood with an example:
Okay, okay, I put that video just because it's fun, but does not explain very well the Coriolis effect.
In this one, we can see that there is an object making a straight path — the pen. However, an observer situated on the circumference that makes a rotational movement will see the pen describing a curved path: the line drawn on the circumference.
The most common example which I think makes people understand very quickly how Coriolis effect works is the Carousel.
This video explains it very well because they show the path seen by an observer outside of the rotation system and another observer inside. Therefore, as one can clearly see, the object describes a straight path while the rotating observer perceives it as a curve.
In these cases, the difference caused by the Coriolis effect is big compared to that produced on Earth since the angular speed of the system in the example is much higher than the one on Earth and the path to examine extends from one side to the other of the system.
This is not the case of drains on Earth, of course. If we had a drain covering almost from one side to the other of an Earth that took a few seconds to turn around itself we would be able to appreciate the Coriolis effect in drains.
To understand why we don't appreciate the Coriolis effect on our tiny drains on our slow Earth, let's go back to the subject of the airplane.
I told above that the Coriolis effect is noticeable in airplanes. And indeed it is very important: if we don't take care of it, we may never reach our destination.
We can see what happens in this animation:
The plane starts its flight in a straight path because it wants to reach a point that it's "in front" of it. But as it goes straight it's destination "escapes" due to the rotation of the Earth. So it has to alter its trajectory and at the end it makes a curved path. This is because the linear velocity of rotation is not the same at all points of the globe. The Earth takes one day to turn around itself at any point on the planet, but the circle it has to describe is much smaller on a pole that on the equator. That is, in the equator travels much farther in the same time, so we can say that as we reach the pole, the [linear] speed of the rotation decreases. The plane begins its path "pushed" by the linear velocity of the rotation of the Earth at the time it takes off, but as we have seen, as it reaches the pole, the linear velocity of rotation decreases, so Earth is "left behind" by the airplane. The Earth does not rotate as fast (note, again, I'm speaking about linear velocity) at the point the plane aims to reach as at the point from which it took off, so the target is not " where we expected."
Well, as told above, this happens because, as the diameter of the circle of rotation of the Earth decreases on the area of the Earth we are, the speed at which it rotates to make a full turn in a day will decrease too. I think that this will make us realize that the difference in the size of the rotation circle in the different points of the drain is not enough to notice the Coriolis effect.
But if my empirical demonstration and "homespun" explanation are not enough for you and you want to know more about this issue with its equations that show how Coriolis effect (not) really affects drains, there is huge information on the net about this topic. For example, in Spanish: The Túzaro, El Tamiz and the aforementioned Axxón magazine. Sorry, I haven't collected links in English.